Pada tahun  1858, di Luxor mesir, Seorang pemburu benda-benda kuno mesir Alexander Henry Rhind, menemukan gulungan kuno dari kertas papirus, Para arkeolog menduga gulungan tersebut ditulis sekitar 1650 SM. Gulungan tersebut berisikan catetan-catetan matematika, seperti rumus luas lingkaran yang dirumuskan 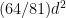  dengan 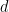adalah diameter lingkaran, sedangkan 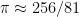. Dari gulungan tersebut diketahui para matematikawan di Masa itu disibukkan dengan permasalahan matematis yang dikenal dengan sebutan Mempersegikan Lingkaran (Squaring the circle).

Dari sebuah lingkaran yang diketahui luasnya, dapatkah kita mengkontruksikan persegi dengan luas yang sama?

Di Jaman sekarang jelas permasalahan diatas dapat diselesaikan  dengan mudahnya melalui bantuan komputer. Akan tetapi di Jaman duhulu alat yang digunakan matematikawan hanyalah Jangka dan Garisan. Okey yang saya maksud dengan garisan adalah penggaris tanpa tanda.

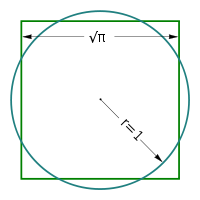
Jika suatu lingkaran mempunyai jari-jari 1 satuan maka lingkaran tersebut mempunyai luas 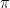persegi maka persegi dengan luas sama akan mempunyai panjang sisi . Jadi mempersegikan lingkaran dapat ditulis ulang sebagai berikut:

Dengan hanya menggunakan jangka dan garisan dapatkah kita membuat garis dengan panjang  satuan?

Para Matematikawan dari masa ke masa tertantang untuk memecahkan masalah tersebut. Pada tahun 1882 muncul Teorema Lindemann–Weierstrass yang menujukan bahwa 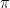adalah bilangan transedental yaitu bukan merupakan akar dari suku banyak berkoefisien bilangan rasional. Dengan adanya teorema tersebut maka terbukti bahwa mempersegikan lingkaran adalah hal yang mustahil. Karena 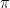  transedental maka dengan sendirinya juga transedental. Bilangan transedental bukanlah bilangan constructible yaitu bilangan yang dapat diperoleh dengan hanya menggunakan jangka dan garisan.

Mmm…bayangkan permasalah matematis yang sudah ada sekitar 1600an SM baru terjawab di tahun 1800an, mencengangkan bukan?

Sekarang ungkapan Mempersegikan lingkaran dijadikan metafora untuk mengatakan sesuatu yang mustahil.

sumber